
Originally Posted by
AndreasBenFenner you have it mixed up.
Boring a motor ups the compression more than stoking a motor. keeping everything else constant.Again, I'm just going off something I read (or remembered possibly incorrectly), but it makes sense to me (obviously that doesn't mean much these days).
I'll do some math of my own. Here's yours.

Originally Posted by
AndreasLook at it like this.
SR20DE 86 piston x 86 crank motor = 1.9983
86 piston x 91 crank = 2.114
91 piston x 86 crank = 2.237
A larger motor with all things being equal will have more compression
That's not what I remember reading. Time to do my own math I guess.
(Skip to the bold stuff for the results. No need to read the rest unless you want to check my work.)
How about this.
Let's assume a flat piston top and a CC volume of 50,000mm³ okay?
A 86mm bore divided by 2 equals a bore radius of 43mm. Use the formula for area of a circle which is Pi times the radius squared. That gives us 3.1459 times 43 squared. 43 squared is 1,849 and then we multiply that by Pi and we get 5,816.7691mm² for the area of the bore. Then we multiply that by the height of the "cylinder" we're trying to get the area of. That's 86mm in height so 5,816.7691mm² times 86mm equals 500,242.1426mm³. That is the area of the cylinder with the piston at the bottom minus the combustion chamber volume. Then we add the combustion chamber volume of 50,000mm³ and we get 550,242.1426mm³. That is the starting volume with the piston at the bottom.
Then with the piston at the top of the stroke, the ending volume is 50,000mm³. Take the larger value and divide by the smaller value and we will have the compression ratio. 550,242.1426mm³ divided by 50,000mm³ equals a compression ratio of
11.0:1 for our pretend stock 86x86 engine.
Now let's do the same thing for just a stroked engine, and then for just a bored engine.
Stroked engine is 91mm stroke with 86mm bore. Same area of the bore circle which was 5,816.7691mm². Then we multiply that by the stroke. That's 91mm this time so 5,816.7691mm² times 91mm equals 529325.9881mm³. That is the area of the cylinder with the piston at the bottom minus the combustion chamber volume. Then we add the combustion chamber volume of 50,000mm³ and we get 579325.9881mm³. That is the starting volume with the piston at the bottom.
Then with the piston at the top of the stroke, the ending volume is 50,000mm³. Take the larger value and divide by the smaller value and we will have the compression ratio. 579325.9881mm³ divided by 50,000mm³ equals a compression ratio of
11.59:1 for our pretend stroked 86x91 engine. That is 0.51 higher than the regular motor by adding 5mm to the stroke.
Now let's add the 5mm to the bore instead.
Bored engine is 86mm stroke with 91mm bore. The area of the bore circle changes now so time to do that math again. Use the formula for area of a circle which is Pi times the radius squared. That gives us 3.1459 times half of 91mm squared. half of 91mm is 45.5mm. 45.5 squared is 2,070.25 and then we multiply that by Pi and we get 6,512.799475mm² for the area of the bore. Then we multiply that by the stroke. That's 86mm this time so 6,512.799475mm² times 86mm equals 560,100.75485mm³. That is the area of the cylinder with the piston at the bottom minus the combustion chamber volume. Then we add the combustion chamber volume of 50,000mm³ and we get 610,100.75485mm³. That is the starting volume with the piston at the bottom.
Then with the piston at the top of the stroke, the ending volume is 50,000mm³. Take the larger value and divide by the smaller value and we will have the compression ratio. 610,100.75485mm³ divided by 50,000mm³ equals a compression ratio of
12.20:1 for our pretend bored 91x86 engine. That is 1.2 higher than the regular motor by adding 5mm to the bore.
And what do you know? You were right. Adding 1mm to the bore significantly raises compression more than adding 1mm to the stroke.
For some fucked up reason this morning when I posted I'd just read this:
Any time you bore or add stroke to an engine, the compression ratio will increase. For example, with everything else remaining the same, building a 383 from a standard-bore 350 changes the compression from 8.6:1 to a stout 9.3:1. Boring the cylinders 0.030-inch increased the compression by only 0.10, but the stroke from 3.48 to 3.75 bumps the compression by 0.60.
from this site:
Engine Compression Guide - Tech Article - Chevy High Performance Magazine
And in the haze before fully waking up I read it incorrectly and thought it said stroke had a larger affect on compression ratio than bore. Obviously I was wrong. Typical I guess. =/
I really need to do my own analysis instead of just trying to read stuff since apparently I have a hard time reading sometimes.

 I prefer discussing things over reading on my own.. it's part of being an extrovert..
I prefer discussing things over reading on my own.. it's part of being an extrovert.. 








 Be the first to like this post.
Be the first to like this post.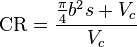




 Back to top
Back to top
